Linha de Alocação de Capital (CAL) e portfólio ideal

A Linha de Alocação de Capital (CAL) é uma linha que representa graficamente o perfil de risco e recompensa dos ativos, e pode ser usado para encontrar o portfólio ideal. O processo de construção da CAL para uma coleção de carteiras é descrito abaixo.

Retorno e variação esperados do portfólio

Para simplificar, vamos construir uma carteira com apenas dois ativos de risco.

O retorno esperado do portfólio é uma média ponderada dos retornos esperados de seus ativos individuais, e é calculado como:

E (Rp) =w ₁ E (R ₁ ) + w ₂ E (R ₂ )

Onde w ₁ , C ₂ são os respectivos pesos para os dois ativos, e E (R ₁ ), E (R ₂ ) são os respectivos retornos esperados.

Os níveis de variação se traduzem diretamente nos níveis de risco; variância mais alta significa níveis mais altos de risco e vice-versa. A variância de uma carteira não é apenas a média ponderada da variância de ativos individuais, mas também depende da covariância e da correlação dos dois ativos. A fórmula para a variação do portfólio é dada como:

Var (R _p ) =w ² ₁ Var (R ₁ ) + w ² ₂ Var (R ₂ ) + 2w ₁ C ₂ Cov (R ₁ , R ₂ )

Onde Cov (R ₁ , R ₂ ) representa a covariância dos dois retornos de ativos. Alternativamente, a fórmula pode ser escrita como:

σ ² _p =w ² ₁ σ ² ₁ + w ² ₂ σ ² ₂ + 2ρ (R ₁ , R ₂ ) C ₁ C ₂ σ ₁ σ ₂ , usando ρ (R ₁ , R ₂ ), a correlação de R ₁ e R ₂ .

A conversão entre correlação e covariância é dada como:ρ (R ₁ , R ₂ ) =Cov (R ₁ , R ₂ ) / σ ₁ σ ₂ .

A variância do retorno do portfólio é maior quando a covariância dos dois ativos é positiva, e menos quando negativo. Uma vez que a variância representa risco, o risco da carteira é menor quando seus componentes de ativos possuem covariância negativa. Diversificação é uma técnica que minimiza o risco da carteira, investindo em ativos com covariância negativa.

Na prática, não sabemos os retornos e desvios-padrão de ativos individuais, mas podemos estimar esses valores com base nos valores históricos desses ativos.

A fronteira eficiente

Uma fronteira de portfólio é um gráfico que mapeia todos os portfólios possíveis com diferentes combinações de peso de ativos, com níveis de desvio padrão da carteira representados graficamente no eixo xe retorno esperado da carteira no eixo y.

Para construir uma fronteira de portfólio, primeiro atribuímos valores para E (R ₁ ), E (R ₂ ), stdev (R ₁ ), stdev (R ₂ ), e ρ (R ₁ , R ₂ ) Usando as fórmulas acima, então calculamos o retorno esperado do portfólio e a variância para cada combinação de peso de ativo possível (w ₂ =1-w ₁ ) Este processo pode ser feito facilmente no Microsoft Excel, conforme mostrado no exemplo abaixo:

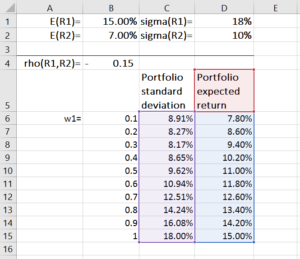
Em seguida, usamos o gráfico de dispersão com linhas suaves para traçar o retorno esperado e o desvio padrão do portfólio. O resultado é mostrado no gráfico abaixo, onde cada ponto no gráfico representa um portfólio construído sob uma combinação de peso de ativo.

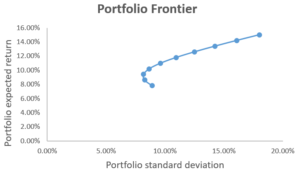
Então, como sabemos quais carteiras são atraentes para os investidores? Para responder a isso, nós introduzimos o conceito de critério de média-variância , que afirma que a Carteira A domina a Carteira B se E (R _UMA ) ≥ E (R _B ) e σ _UMA ≤ σ _B (ou seja, a carteira A oferece um maior retorno esperado e menor risco do que a carteira B). Se for esse o caso, então os investidores prefeririam A a B.

No gráfico, podemos inferir que as carteiras na parte com inclinação para baixo da fronteira da carteira são dominadas pela parte com inclinação para cima. Como tal, os pontos na parte inclinada para cima da fronteira da carteira representam carteiras que os investidores consideram atraentes, enquanto os pontos na parte inclinada para baixo representam carteiras que são ineficientes.

De acordo com o critério de média-variância, qualquer investidor selecionaria de forma ideal uma carteira na parte com inclinação ascendente da fronteira da carteira, que é chamado de fronteira eficiente , ou fronteira de variância mínima . A escolha de qualquer carteira na fronteira eficiente depende das preferências de risco do investidor.

Um portfólio acima da fronteira eficiente é impossível, enquanto um portfólio abaixo da fronteira eficiente é ineficiente.

Portfólio completo e linha de alocação de capital

Na construção de carteiras, os investidores costumam combinar ativos de risco com ativos sem risco (como títulos do governo) para reduzir os riscos. Um portfólio completo é definido como uma combinação de um portfólio de ativos de risco, com retorno R _p , e o ativo livre de risco, com retorno R _f .

O retorno esperado de um portfólio completo é dado como:

E (R _c ) =w _p E (R _p ) + (1 - w _p ) R _f

E a variância e o desvio padrão do retorno completo da carteira são dados como:

Var (R _c ) =w ² _p Var (R _p ), σ (R _c ) =w _p σ (R _p ),

onde w _p é a fração investida na carteira de ativos de risco.

Enquanto o excesso de retorno esperado de um portfólio completo é calculado como:

E (R _c ) - R _f ,

se substituirmos E (R _c ) com a fórmula anterior, nós pegamos w _p (E (R _p ) - R _f )

O desvio padrão do portfólio completo é σ (R _c ) =w _p σ (R _p ), o que nos dá:

C _p =σ (R _c ) / σ (R _p )

Portanto, para cada portfólio completo:

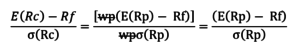
Ou E (R _c ) =R _f + S _p σ (R _c ), Onde está a _p =

A linha E (R _c ) =R _f + S _p σ (R _c ) é a linha de alocação de capital (CAL). A inclinação da linha, S _p , é chamado de Razão de Sharpe Índice de Sharpe O Índice de Sharpe é uma medida de retorno ajustado ao risco, que compara o excesso de retorno de um investimento com seu desvio padrão de retornos. O Índice de Sharpe é comumente usado para avaliar o desempenho de um investimento ajustando seu risco., ou relação recompensa-risco. O índice de Sharpe mede o aumento no retorno esperado por unidade de desvio padrão adicional.

Portfólio ideal

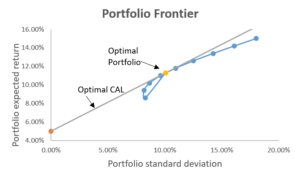
O portfólio ideal consiste em um ativo livre de risco e um portfólio ideal de ativos de risco. O portfólio de ativos de risco ideal está no ponto onde a CAL é tangente à fronteira eficiente. Este portfólio é ideal porque a inclinação da CAL é a mais alta, o que significa que alcançamos os maiores retornos por unidade adicional de risco. O gráfico abaixo ilustra isso:

Os pesos tangentes do portfólio são calculados da seguinte forma:

Resumo da linha de alocação de capital

Os investidores usam a fronteira eficiente e a CAL para obter diferentes combinações de risco e retorno com base no que desejam. O portfólio de risco ideal é encontrado no ponto onde a CAL é tangente à fronteira eficiente. Esta combinação de peso de ativos dá a melhor relação risco-recompensa, pois tem a maior inclinação para CAL.

Baixe o modelo grátis

Digite seu nome e email no formulário abaixo e baixe o template grátis agora!

Recursos adicionais

Obrigado por ler o guia do CFI para a linha de alocação de capital. Para progredir em sua carreira como Analista de Modelagem e Avaliação FinanceiraTorne-se um Analista de Avaliação e Modelagem Financeira (FMVA) ®A certificação de Analista de Modelagem e Avaliação Financeira (FMVA) ® do CFI o ajudará a ganhar a confiança necessária em sua carreira financeira. Inscreva-se hoje !, esses recursos adicionais serão úteis:

• Perfil de carreira de gerenciamento de portfólioGestão de portfólio Perfil de carreira A gestão de portfólio é o gerenciamento de investimentos e ativos para clientes, que incluem fundos de pensão, bancos, fundos de hedge, escritórios familiares. O gerente de portfólio é responsável por manter a combinação de ativos adequada e estratégia de investimento que atenda às necessidades do cliente. Salário, Habilidades,
• Prêmio de risco de mercado Prêmio de risco de mercado O prêmio de risco de mercado é o retorno adicional que um investidor espera de manter uma carteira de mercado arriscada em vez de ativos sem risco.
• Definição do índice de Sharpe Índice de Sharpe O índice de Sharpe é uma medida de retorno ajustado ao risco, que compara o excesso de retorno de um investimento com seu desvio padrão de retornos. O Índice de Sharpe é comumente usado para avaliar o desempenho de um investimento ajustando seu risco.
• Calculadora de proporção de SharpeCalculadora de proporção de SharpeA Calculadora de proporção de Sharpe permite medir o retorno ajustado ao risco de um investimento. Baixe o modelo do CFI em Excel e a calculadora Sharpe Ratio. Razão de Sharpe =(Rx - Rf) / StdDev Rx. Onde:Rx =retorno esperado do portfólio, Rf =Taxa de retorno livre de risco, StdDev Rx =Desvio padrão do retorno / volatilidade da carteira