As diferenças entre o simples vs. Juros compostos

Os juros sobre contas de poupança e outros tipos de contas são calculados usando juros simples ou compostos. Os juros simples são calculados apenas sobre o valor do depósito, enquanto os juros compostos são calculados sobre o principal, mais juros. Mais juros são ganhos sobre os depósitos quando o método de composição é usado.
Explicação
A principal diferença entre juros simples e compostos é que os juros simples são calculados apenas sobre o valor do depósito. Juros simples nunca são calculados sobre os juros ganhos anteriormente. Por causa disso, os juros compostos geram valores mais elevados.
Simples interesse
Os juros simples são calculados sobre os depósitos usando a seguinte fórmula:Juros =Principal vezes taxa vezes tempo (I =PRT). Com juros simples, os montantes de juros são geralmente calculados apenas uma vez. Por exemplo, se uma pessoa comprou um certificado de depósito de $ 500 (CD) que contém uma taxa de juros simples de seis por cento e é um depósito de dois anos, é calculado usando a fórmula de juros simples. Para calcular o valor dos juros ganhos pelo depositante, a equação é:I =($ 500) x (6%) x (2). Os juros ganhos nos dois anos são de $ 60. Quando a pessoa resgata este CD, ele recebe $ 560.
Juros compostos
Os juros compostos são os juros ganhos em depósitos mais os juros ganhos anteriormente. Quando um depósito rende juros compostos, o valor do investimento cresce mais rápido. Os juros são calculados várias vezes, dependendo do investimento. Os juros compostos podem ser compostos diariamente, semanalmente, por mês, trimestral ou anual. Se o CD do exemplo acima tiver juros compostos calculados anualmente, os juros são calculados de forma diferente do que estava acima. A mesma fórmula é usada duas vezes. A primeira vez que os juros são calculados é no final do primeiro ano, usando a mesma fórmula:I =($ 500) x (6%) x (1). A resposta é $ 30. O investimento vale $ 530 no final do primeiro ano.
No final do segundo ano, o valor principal muda. Como resultado, a equação muda:I =($ 530) x (6%) x (1). Esta resposta, $ 561,80, reflete o valor total do investimento após o segundo ano.
Diferenças no exemplo
A diferença nas respostas é causada pela diferença em como o valor dos juros é calculado. O mesmo investimento vale mais dinheiro quando os juros são compostos. A diferença neste exemplo é mínima, mas conforme o número de anos do investimento aumenta, a diferença pode produzir resultados mais variados.
Artigos em Destaque
- As diferenças entre uma letra de câmbio,
- As diferenças entre verificação pessoal e comercial
- As diferenças entre EBITA e EBITDA e EPS
- As diferenças entre seguro e resseguro
- Juros simples vs. juros compostos:as principais diferenças
- A magia dos juros compostos
- Qual é a ligação entre fundos mútuos e juros compostos?
- Um guia para juros simples vs. Juros compostos
-
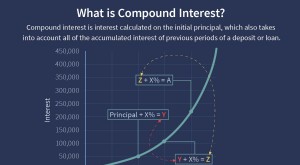 Juros compostos
Juros compostos O que são juros compostos? Juros compostos (ou juros compostos) são os juros de um empréstimo ou depósito calculados com base no principal inicial e nos juros acumulados de períodos anteriores. Acre...
-
 Qual é a fórmula de juros compostos?
Qual é a fórmula de juros compostos? p Para iniciar, é importante entender primeiro o que são juros compostos. Os juros compostos são retirados do valor inicial - ou principal - de um empréstimo ou depósito, mais quaisquer juros que já t...


