O que é Retorno Composto Continuamente?

Retorno composto continuamente é o que acontece quando os juros ganhos em um investimento são calculados e reinvestidos na conta por um número infinito de períodos. Os juros são calculados sobre o valor do principal e os juros acumulados ao longo dos períodos dados e reinvestidos no saldo de caixa.

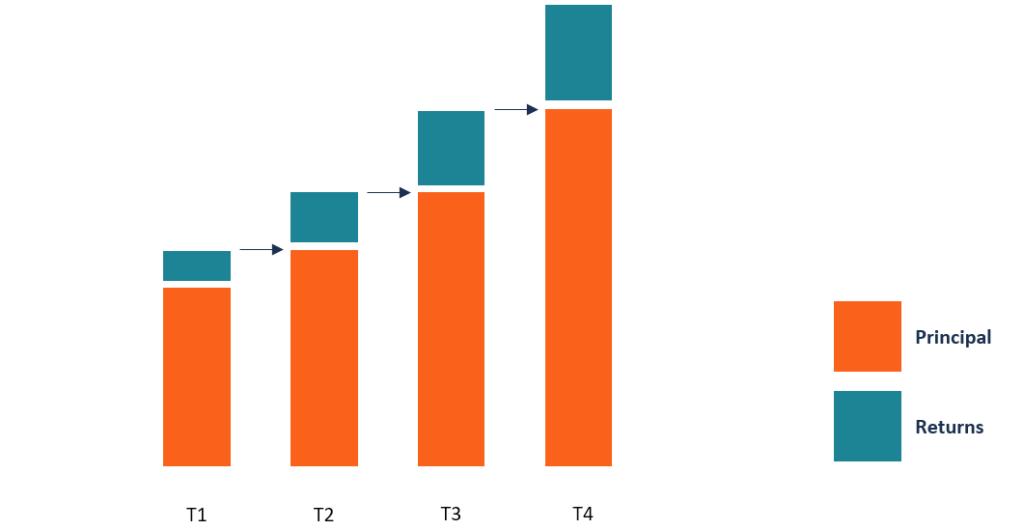
A composição regular é calculada em intervalos de tempo específicos, como mensal, trimestral, semestralmente e anualmente. A composição contínua é um caso extremo desse tipo de composição, uma vez que calcula juros ao longo de um número infinito de períodos, em vez de assumir um número específico de períodos. A diferença entre os juros obtidos por meio do método de composição tradicional e o método de composição contínua pode ser significativa.

Retorno Composto Anual vs. Retorno Composto Contínuo

Os investidores calculam os juros ou a taxa de retorno Taxa de retorno A taxa de retorno (ROR) é o ganho ou a perda de um investimento durante um período de tempo associado ao custo inicial do investimento expresso como uma porcentagem. Este guia ensina as fórmulas mais comuns sobre seus investimentos usando duas técnicas principais:composição anual e composição contínua.

Composição anual

A composição anual significa que o retorno sobre um investimento é calculado a cada ano, e é diferente de juros simples. O método de composição anual usa a seguinte fórmula:

Total =[Principal x (1 + Juros)] ^ Número de anos

O retorno do investimento é obtido deduzindo o valor do principal do retorno total obtido pela fórmula acima.

Suponha que a Empresa ABC investiu $ 10, 000 para comprar um instrumento financeiro, e a taxa de retorno é de 5% por dois anos. Portanto, os juros ganhos com o investimento da ABC para o período de dois anos são os seguintes:

=[10, 000 x (1 + 0,05) ^ 2

=(10, 000 x 1,1025)

=11, 025 - 10, 000

= $ 1, 025

Portanto, A empresa ABC ganhou juros de $ 1, 025 em seu investimento de $ 10, 000 ao longo de dois anos.

Retorno Composto Contínuo

Ao contrário da composição anual, que envolve um número específico de períodos, o número de períodos usados ​​para composição contínua é infinitamente numeroso. Em vez de usar o número de anos na equação, a composição contínua usa uma constante exponencial para representar o número infinito de períodos. A fórmula para o principal mais juros é a seguinte:

Total =Principal x e ^ (Juros x Anos)

Onde:

• e - a função exponencial, que é igual a 2,71828.

Usando o exemplo da Empresa ABC acima, o retorno sobre o investimento pode ser calculado da seguinte forma, ao usar composição contínua:

=10, 000 x 2,71828 ^ (0,05 x 2)

=10, 000 x 1,1052

= $ 11, 052

Juros =$ 11, 052 - $ 10, 000

= $ 1, 052

A diferença entre o retorno do investimentoReturn on Investment (ROI) Return on Investment (ROI) é uma medida de desempenho usada para avaliar o retorno de um investimento ou comparar a eficiência de diferentes investimentos. ao usar a capitalização contínua versus a capitalização anual é de $ 27 ($ 1, 052 - $ 1025).

Diário, Por mês, Trimestral, e composição semestral

Além dos métodos de composição anuais e contínuos, os juros também podem ser compostos em diferentes intervalos de tempo, como diariamente, por mês, trimestral e semestralmente.

Para ilustrar a composição em diferentes intervalos de tempo, tomamos um investimento inicial de $ 1, 000 que paga uma taxa de juros; Taxa de juros; Uma taxa de juros refere-se ao valor cobrado por um credor a um mutuário por qualquer forma de dívida concedida, geralmente expressa como uma porcentagem do principal. de 8%.

Composição diária

A fórmula para composição diária é a seguinte:

=Principal x (1 + juros / 365) ^ 365

=1, 000 x (1 + 0,08 / 365) ^ 365

=1, 000 x (1 + 0,00022) ^ 365

=1, 000 x (1.00022) ^ 365

=1, 000 x 1,0836

= $ 1, 083,60

Composição mensal

A fórmula para os intervalos mensais é a seguinte:

=Principal x (1 + juros / 12) ^ 12

=1, 000 x (1 + 0,08 / 12) ^ 12

=1, 000 x [1 + 0,0067) ^ 12

=1, 000 x (1,0067) ^ 12

=1, 000 x (1,083)

= $ 1, 083,00

Composição trimestral

A fórmula para composição trimestral é a seguinte:

=Principal x (1 + juros / 4) ^ 4

=1, 000 x (1 + 0,08 / 4) ^ 4

=1, 000 x (1 + 0,02) ^ 4

=1, 000 x (1,02) ^ 4

=1, 000 x 1,0824

= $ 1, 082,40

Composição semestral

A fórmula para composição semestral é a seguinte:

=Principal x (1 + juros / 2) ^ 2

=1, 000 x (1 + 0,08 / 2) ^ 2

=1, 000 x (1 + 0,04) ^ 2

=1, 000 x (1,04) ^ 2

=1, 000 x 1,0816

= $ 1, 081,60

Conclusão sobre os intervalos de composição

A partir dos cálculos acima, podemos concluir que todos os intervalos produzem um interesse quase igual, mas com uma pequena variação. Por exemplo, a composição trimestral produz juros de $ 82,40, que é um pouco mais alto do que os juros produzidos pela composição semestral em $ 81,60.

Também, a taxa mensal rende juros de $ 83, que é um pouco mais alto do que os juros produzidos pelas taxas trimestrais de $ 82,40. A composição diária rende juros mais altos de $ 83,60, que é um pouco mais alto do que os juros mensais de $ 82,60.

Do padrão acima, também podemos dizer que pequenos intervalos compostos de juros produzem taxas de juros mais altas em comparação com grandes intervalos compostos.

Importância da Composição Contínua

A composição contínua oferece vários benefícios em relação aos juros simplesJuros simplesFórmula de juros simples, definição e exemplo. Juros simples é um cálculo de juros que não leva em consideração o efeito da composição. Em muitos casos, compostos de juros com cada período designado de um empréstimo, mas no caso de juros simples, isso não. O cálculo dos juros simples é igual ao valor do principal multiplicado pela taxa de juros, multiplicado pelo número de períodos. e composição regular. Os benefícios incluem:

1. Reinvestir os ganhos perpetuamente

Um dos benefícios da composição contínua é que os juros são reinvestidos na conta por um número infinito de períodos. Isso significa que os investidores desfrutam do crescimento contínuo de suas carteiras, em comparação com quando eles ganham juros mensalmente, trimestral, ou anualmente com composição regular.

2. O valor dos juros continuará crescendo

Na composição contínua, tanto o interesse quanto o principal continuam crescendo, o que facilita a multiplicação dos retornos no longo prazo. Outras formas de composição rendem apenas juros sobre o principal e esses juros são pagos à medida que são ganhos. Reinvestir os juros permite ao investidor ganhar a uma taxa exponencial por um número infinito de períodos.

Recursos adicionais

Obrigado por ler a explicação do CFI sobre retorno composto continuamente. A CFI oferece o Financial Modeling &Valuation Analyst (FMVA) ™ Torne-se um Certified Financial Modeling &Valuation Analyst (FMVA) ® A certificação do Financial Modeling and Valuation Analyst (FMVA) ® o ajudará a ganhar a confiança necessária em sua carreira financeira. Inscreva-se hoje! programa de certificação para aqueles que procuram levar suas carreiras para o próximo nível. Para continuar aprendendo e progredindo em sua carreira, os seguintes recursos CFI serão úteis:

• Taxa de porcentagem anual (APR) Taxa de porcentagem anual (APR) A taxa de porcentagem anual (APR) é a taxa anual de juros que um indivíduo deve pagar sobre um empréstimo, ou que eles recebem em uma conta de depósito. Em última análise, APR é um termo percentual simples usado para expressar o valor numérico pago por um indivíduo ou entidade anualmente pelo privilégio de tomar dinheiro emprestado.
• Taxa composta de crescimento anual (CAGR) CAGRCAGR significa Taxa composta de crescimento anual. É uma medida da taxa de crescimento anual de um investimento ao longo do tempo, com a composição levada em consideração.
• Calculadora de taxas de juros Calculadora de taxas de juros Calculadora de taxas de juros para ajudá-lo a calcular a taxa de juros efetiva com base no número de períodos, tipo de taxa de juros, e o valor do saldo inicial.
• Pagamento PrincipalPagamento Principal Um pagamento principal é um pagamento referente ao valor original de um empréstimo devido. Em outras palavras, um pagamento principal é um pagamento feito em um empréstimo que reduz o valor restante do empréstimo devido, em vez de aplicar para o pagamento de juros cobrados sobre o empréstimo.