Paridade Put-Call
O que é paridade Put-Call?
O termo paridade "put-call" refere-se a um princípio que define a relação entre o preço de opções europeias de venda e de compra da mesma classe. Simplificando, este conceito destaca as consistências dessas mesmas classes. As opções de venda e compra devem ter o mesmo ativo subjacente, preço de exercício, e data de validade para pertencer à mesma classe. A paridade put-call, que se aplica apenas às opções europeias, pode ser determinado por uma equação definida.
Principais vantagens
- A paridade de venda e de venda mostra a relação que deve existir entre as opções de venda e compra europeias que têm o mesmo ativo subjacente, expiração, e preços de exercício.
- Este conceito diz que o preço de uma opção de compra implica um determinado preço justo para a opção de venda correspondente com o mesmo preço de exercício e vencimento e vice-versa.
- A paridade put-call não se aplica às opções americanas porque você pode exercê-las antes da data de vencimento.
- Se a paridade put-call for violada, então surgem oportunidades de arbitragem.
- Você pode determinar a chamada inicial usando a fórmula C + PV (x) =P + S.
Paridade Put-Call
Compreendendo a Paridade Put-Call
Como observado acima, a paridade put-call é um conceito que se aplica às opções europeias. Essas opções são da mesma classe, o que significa que eles têm o ativo subjacente, preço de exercício, e data de validade. Como tal, o princípio não se aplica às opções americanas, que pode ser exercido a qualquer momento antes da data de expiração.
A paridade de compra e de venda afirma que manter simultaneamente uma opção de venda curta europeia e uma opção de compra longa europeia da mesma classe proporcionará o mesmo retorno que a manutenção de um contrato a termo no mesmo ativo subjacente, com a mesma expiração, e um preço futuro igual ao preço de exercício da opção.
Se os preços das opções de compra e venda divergem de modo que essa relação não se mantenha, existe uma oportunidade de arbitragem. Isso significa que os traders sofisticados podem teoricamente obter um lucro sem risco. Essas oportunidades são incomuns e de curta duração em mercados líquidos.
A equação que expressa a paridade put-call é:
C + PV (x) =P + S
Onde:
C =preço da opção de compra europeia
PV (x) =o valor presente do preço de exercício (x), descontado do valor na data de vencimento pela taxa livre de risco
P =preço da opção de venda europeia
S =preço à vista ou valor de mercado atual do ativo subjacente
p O conceito de paridade put-call foi introduzido pelo economista Hans R. Stoll em seu artigo de dezembro de 1969 "The Relationship Between Put and Call Option Price, "que foi publicado em The Journal of Finance .
Considerações Especiais
Quando um lado da equação de paridade put-call é maior do que o outro, isso representa uma oportunidade de arbitragem. Você pode vender o lado mais caro da equação e comprar o lado mais barato para fazer, para todos os efeitos, um lucro sem risco.
Na prática, isso significa vender uma opção de venda, vendendo ações, comprando uma ligação, e comprar o ativo livre de risco (TIPS, por exemplo). Na realidade, as oportunidades de arbitragem duram pouco e são difíceis de encontrar. Além disso, as margens que oferecem podem ser tão reduzidas que uma enorme quantidade de capital é necessária para aproveitá-las.
Paridade Put-Call e Arbitragem
Nos dois gráficos acima, a y- eixo representa o valor do portfólio, não o lucro ou perda, porque presumimos que os comerciantes dão opções de graça. Mas isso não acontece e os preços das opções de venda e compra europeias são, em última análise, regidos pela paridade de venda e compra. Teoricamente, mercado perfeitamente eficiente, os preços das opções de compra e venda europeias seriam regidos pela equação que observamos acima:
C + PV (x) =P + S
Digamos que a taxa livre de risco seja de 4% e que as ações TCKR sejam negociadas a $ 10. Vamos continuar a ignorar as taxas de transação e assumir que TCKR não paga dividendos. Para opções TCKR com vencimento em um ano e preço de exercício de $ 15, temos:
C + (15 ÷ 1,04) =P + 10
4,42 =P - C
Neste mercado hipotético, As opções de venda TCKR devem ser negociadas com um prêmio de $ 4,42 para suas opções de compra correspondentes. Com o TCKR sendo negociado a apenas 67% do preço de exercício, a chamada de alta parece ter as chances mais longas, o que faz sentido intuitivamente. Digamos que não seja o caso, no entanto, Por qualquer motivo, as opções de venda estão sendo negociadas a $ 12, as chamadas em $ 7.
Digamos que você compre uma opção de compra europeia para ações TCKR. A data de validade é daqui a um ano, o preço de exercício é $ 15, e comprar a ligação custa $ 5. Este contrato dá a você o direito, mas não a obrigação, de comprar ações TCKR na data de vencimento por $ 15, qualquer que seja o preço de mercado.
Se daqui a um ano, TCKR negocia a $ 10, você não exercerá a opção. Se, por outro lado, TCKR está sendo negociado a $ 20 por ação, você vai exercer a opção, compre TCKR por $ 15 e ponto de equilíbrio, já que você pagou $ 5 pela opção inicialmente. Qualquer valor de TCKR acima de $ 20 é puro lucro, assumindo zero taxas de transação.
7 + 14,42 <12 + 10
21,42 chamada fiduciária <22 posto protegido
Colocação de proteção
Outra forma de imaginar a paridade put-call é comparar o desempenho de uma put de proteção e uma chamada fiduciária da mesma classe. Uma opção de venda de proteção é uma posição de estoque longa combinada com uma opção de venda longa, que atua para limitar o lado negativo de manter o estoque.
Chamada Fiduciária
Uma opção de compra fiduciária é uma opção de compra combinada com dinheiro igual ao valor presente (ajustado pela taxa de desconto) do preço de exercício; isso garante que o investidor tenha caixa suficiente para exercer a opção na data de vencimento. Antes, dissemos que opções de compra e venda de TCKR com preço de exercício de $ 15, expirando em um ano, ambas negociadas a $ 5, mas vamos supor por um segundo que eles sejam negociados de graça.
Exemplo de paridade put-call
Digamos que você também venda (ou "venda" ou "venda a descoberto") uma opção de venda europeia para ações TCKR. A data de expiração, preço de exercício, e o custo da opção são os mesmos. Você recebe $ 5 por assinar a opção, e não cabe a você exercer ou não a opção, uma vez que você não a possui. O comprador compra o direito, mas não a obrigação, para vender ações TCKR ao preço de exercício. Isso significa que você é obrigado a fazer esse negócio, qualquer que seja o preço da participação de mercado do TCKR.
Portanto, se o TCKR for negociado a US $ 10 por ano a partir de agora, o comprador vende as ações a $ 15. Ambos estão no ponto de equilíbrio - você já ganhou $ 5 com a venda da opção de venda, compensando seu déficit, enquanto o comprador já gastou $ 5 para comprá-lo, comendo seu ganho. Se o TCKR for negociado a $ 15 ou mais, você ganha $ 5 e apenas $ 5, uma vez que a outra parte não exerce a opção. Se o TCKR for negociado abaixo de $ 10, você perde dinheiro - até $ 10, se TCKR vai para zero.
O lucro ou perda nessas posições para diferentes preços de ações TCKR é destacado no gráfico diretamente acima desta seção. Observe que, se você adicionar o lucro ou prejuízo da opção de compra longa ao da opção de venda curta, você ganha ou perde exatamente o que teria se tivesse simplesmente assinado um contrato a termo de ações TCKR a $ 15, expirando em um ano. Se as ações custarem menos de US $ 15, você perde dinheiro. Se eles querem mais, você ganha. Novamente, este cenário ignora todas as taxas de transação.
Outra forma de imaginar a paridade put-call é comparar o desempenho de uma put de proteção e uma chamada fiduciária da mesma classe. Uma opção de venda de proteção é uma posição de estoque longa combinada com uma opção de venda longa, que atua para limitar o lado negativo de manter o estoque.
Uma opção de compra fiduciária é uma opção de compra combinada com dinheiro igual ao valor presente (ajustado pela taxa de desconto) do preço de exercício; isso garante que o investidor tenha caixa suficiente para exercer a opção na data de vencimento. Antes, dissemos que opções de compra e venda de TCKR com preço de exercício de $ 15, expirando em um ano, ambas negociadas a $ 5, mas vamos supor por um segundo que eles sejam negociados de graça.
Por que a paridade Put-Call é importante?
p A paridade put-call permite calcular o valor aproximado de uma put ou call em relação a seus outros componentes. Se a paridade put-call for violada, o que significa que os preços das opções de compra e venda divergem, de modo que esta relação não se mantém, existe uma oportunidade de arbitragem. Embora essas oportunidades sejam incomuns e de curta duração em mercados líquidos, operadores sofisticados podem teoricamente obter um lucro sem risco. Além disso, oferece flexibilidade para criar posições sintéticas.Qual é a fórmula para a paridade put-call?
p A paridade de venda e de venda estabelece que a compra e venda simultânea de uma opção de compra e venda europeia da mesma classe (mesmo ativo subjacente, preço de exercício, e data de expiração) é idêntica à compra do ativo subjacente agora. O inverso dessa relação também seria verdadeiro.Preço da Opção de Compra + PV (x) =Preço da Opção de Venda + Preço Atual do Ativo Subjacentep -ou-
Preço atual do ativo subjacente =Preço da opção de compra - Preço da opção de venda + PV (x)p onde:PV (x) =o valor presente do preço de exercício (x), descontado do valor na data de vencimento pela taxa livre de risco
Como as opções são precificadas?
p O preço de uma opção é a soma de seu valor intrínseco, que é a diferença entre o preço atual do ativo subjacente e o preço de exercício da opção, e valor de tempo, que está diretamente relacionado ao tempo restante até o vencimento dessa opção. pp Hoje em dia, o preço de uma opção é determinado usando modelos matemáticos, como o conhecido Black-Scholes-Merton (BSM). Depois de inserir o preço de exercício de uma opção, o preço atual do instrumento subjacente, tempo para expirar, taxa livre de risco, e volatilidade, este modelo cuspirá o valor justo de mercado da opção.
Artigos em Destaque
-
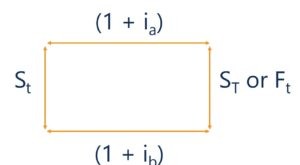 O que é a Paridade da Taxa de Juros (IRP)?
O que é a Paridade da Taxa de Juros (IRP)? A paridade da taxa de juros (IRP) é uma teoria sobre a relação entre a taxa de câmbio à vista. Preço local. O preço à vista é o preço de mercado atual de um título, moeda, ou mercadoria disponível par...
-
 O que é Paridade da Taxa de Juros Coberta (CIRP)?
O que é Paridade da Taxa de Juros Coberta (CIRP)? p A paridade da taxa de juros coberta (CIRP) é uma condição financeira teórica que define a relação entre as taxas de juros e as taxas de câmbio à vista e a prazo de dois países. Estabelece o fato de ...


